By Minhao He, 2020 CEI Graduate Fellow | PDF download
Overview
Students explore the alignment of lattices of layers of graphite graphically to reveal emergent patterns.
Essential Question
How does a superlattice form when stacking two layers of 2D materials?
Background
After the discovery of graphene in 2004, a huge family of two-dimensional materials have been identified and realized in recent decade, covering a wide category of materials from normal metals, semiconductors, and insulators, to materials with more exotic phases, like magnets and superconductors. An ongoing effort in the field is to build heterostructures with different 2D materials as building blocks, to realize material systems with even more exotic properties or to match application goals.
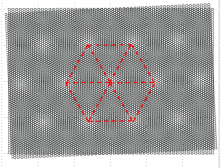
When stacking two layers of 2D materials together, it is important to control the alignment of the crystalline axis of the two layers. A small misalignment in the crystalline axis results in a superlattice on a much larger scale compared with the original lattice unit cell. This superlattice is known as a Moire superlattice and has a fundamental role in heterostructures with a small twist angle. Recently, it has been shown that when stacking two monolayers of graphene together with an twist angle close to 1.1 degrees, the Moire superlattice gives rise to unique flat electronic bands near fermi surface and results in numerous strongly correlated phases, such as correlated insulator, superconductivity, ferromagnetism and topological Chern insulator.
This demo aims to introduce the concept of a Moire superlattice, and visualize its formation and relation with twist angle. This demo only uses graphene and h-BN as example.
Research Connection
This demo is very closely related to cutting-edge research ongoing in the labs of Xiaodong Xu and Matthew Yankowitz.
NGSS Standards
| Number | Description |
| HS-PS2-6 | Communicate scientific and technical information about why the molecular-level structure is important in the functioning of designed materials. |
| SEP2 | Developing and using models |
| CC 1 | Patterns |
Materials
- Graphene lattice structure printed on transparency films, or a PowerPoint model.
- hBN lattice printed on transparency films with the same structure, lattice constant 5% larger than graphene lattice. In reality, the hBN lattice constant is only 1.8% larger than graphene, but here we assume the difference is 5% for visual clarity.
Procedure
- How does a superlattice form when stacking two layer of 2D materials?
- What is the relation between the period of the superlattice (Moire period, d) and twist angle theta)?
- For every 60 degree twist angle rotation, the superlattice become the same (six fold rotational symmetry)
- Within 0 to 60 degree, the larger twist angle is, the smaller Moire period is.
- For quantitative relation between d and theta
- d=alpha/ 2 sin (theta/2), where a is the lattice constant of graphene (a=0.246nm, in reality)
- What is the difference between a graphene-graphene Moire pattern and a graphene-hBN Moire pattern? For a graphene-graphene Moire pattern, there is no superlattice formed with a twist angle of 0. But for graphene-hBN, even at a twist angle of 0, there is a superlattice.
- How to understand that Moire pattern would change the electronic and optical properties of the materials systems? (from a very naïve way) Upon forming the Moire pattern, the lattice structure can be categorized as AA sites and AB/BA sites on a large scale. When electron move inside this crystal, it feels different potential on AA sites and AB/BA sites, therefore it will have preference to reside not uniformly in the lattice but on AA site only.
References:
- Seyler, K.L., Rivera, P., Yu, H. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019). https://doi.org/10.1038/s41586-019-0957-1
- He, M. et al. Tunable correlation-driven symmetry breaking in twisted double bilayer graphene. arXiv:2002.08904.
- Chen, S. He, M et al. Electrically tunable correlated and topological states in twisted monolayer-bilayer graphene. https://arxiv.org/abs/2004.11340